지난 글에 이어서 포트폴리오의 기하수익률을 높이기 위해 비중을 조절해 투자하는 방법을 소개해 보겠다. ‘섀넌의 도깨비’라고 불리는 ‘균형 복원 포트폴리오’가 대표적인 예다.

‘클로드 섀넌(Claude Elwood Sha-nnon)’은 미국의 응용수학자이자 컴퓨터과학자다. 최초로 0과 1의 2진법으로 구성된 ‘비트(bit)’라는 용어를 만들고 비트를 통해 문자와 소리, 이미지 등의 정보를 전달하는 방법을 고안했다. 그는 <수학적 커뮤니케이션 이론, The Mathematical Theory of Communication>을 발표해서 정보이론의 기초를 확립했다. 섀넌은 이 논문에서 전화선 등을 통해 소리와 같은 정보가 전달될 때 자연적으로 각종 오류와 노이즈가 발생할 수밖에 없다고 하는 통념을 깨고, 디지털화된 정보가 잡음 없이 원하는 장소에 정확하게 전달될 수 있음을 이론적으로 증명했다.

그는 미국의 전자통신시대 시작의 중심에 있었으며 ‘디지털의 아버지’라고 불렸다. 인류가 최초로 컴퓨터를 발명하게 된 하드웨어적인 창시자가 앨런 튜링이라면 소프트웨어적인 창시자는 클로드 섀넌이라고 할 수 있다.

섀넌은 수학, 컴퓨터, 인공지능, 암호학, 엔트로피 이론 등에 많은 업적을 남겼다. 섀넌의 ‘정보이론’은 노이즈 속에 숨어있는 정보에 관한 것으로, 현대 통신의 이론적 기반을 제공한다. 정보이론과 주식투자는 얼핏 보기에는 별 상관이 없어 보이지만 노이즈 속에 숨어있는 정보에 집중한다는 주제에서 접점이 있다. 섀넌은 주식투자에도 많은 관심을 기울였는데, 그중 ‘섀넌의 주사위게임’, ‘섀넌의 도깨비’라고 불리는 ‘균형 복원 포트폴리오’가 유명하다.

‘섀넌의 도깨비’

섀넌은 랜덤워크(Random Walk)로 움직이는 주식시장에서 포트폴리오 분산과 조정을 통해 시장의 평균수익률을 이길 수 있는 방법을 제시했다. 섀넌의 주장은 주가는 랜덤워크를 따르며 그래서 시장은 합리적이라는 효율적 시장가설을 정면으로 반박하는 것이었다.

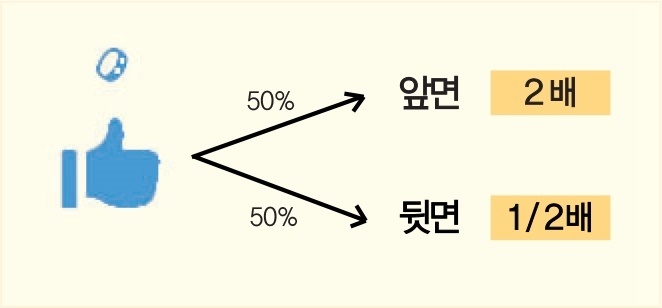
아주 단순한 동전던지기 게임을 생각해보자. 이 동전던지기 게임은 앞면과 뒷면이 나올 확률이 각각 반반이며, 투자자는 동전을 던져서 앞면이 나오면 2배를 받고, 뒷면이 나오면 반만 돌려받는 게임을 계속한다. 즉, 매번 100%의 이익을 보거나 50%의 손실을 본다.

예를 들어 100원의 투자금으로 동전던지기 게임을 시작하면, 앞면이 나오면 100원을 획득하게 돼서 200원이 되고, 뒷면이 나오면 50원이 된다. 이 게임의 산술평균 기댓값은 1.75이지만 기하평균 기댓값은 1.0이다. 동전던지기 게임을 무한대로 시뮬레이션 해볼수록 기하평균 기댓값에 수렴하고 원금이 그대로인 것을 알 수 있으며, 동전던지기의 특성상 이 게임은 랜덤워크를 따른다고 할 수 있다.

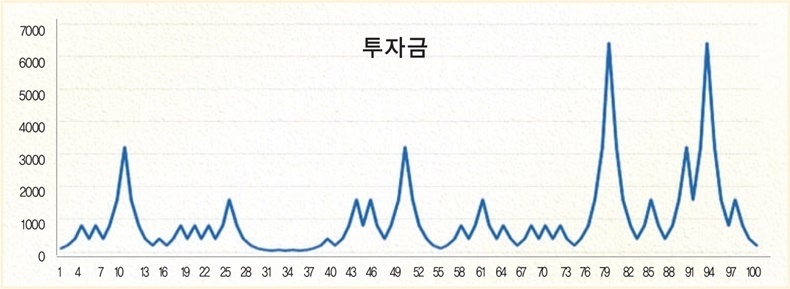
만약 100원의 투자금을 걸고 게임을 시작한다면 운이 좋아 돈이 불어날 때도 있지만 반대로 돈을 계속 잃기도 한다. 이 게임의 변동성은 크지만, 장기수익률은 0에 가깝다(기하평균 기댓값이 0이기 때문). 섀넌은 이 게임을 진행할 때 자신이 가지고 있는 투자금의 절반만 투자해서 게임을 한다면 단기적으로는 결과를 예측할 수 없지만, 장기적으로는 엄청난 수익을 달성할 수 있다고 했다. 매번 주사위를 던질 때마다 자신의 전체 자산의 50%만 이 게임에 투자하며, 나머지 절반은 현금으로 보유한다. 이러한 50:50 리밸런싱 전략을 사용해서 같은 결과에 대입시켜봤더니 아래와 같이 투자금이 우상향하는 것을 볼 수 있다.

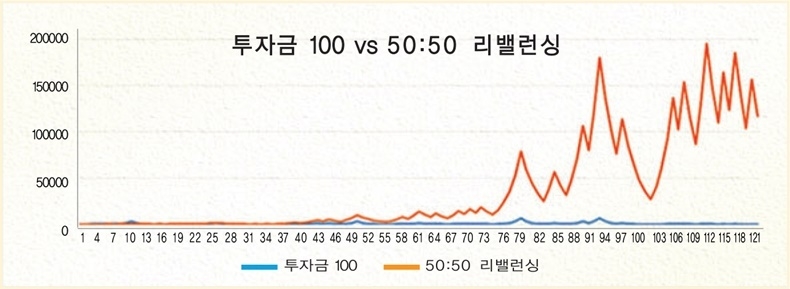
위의 결과에서 보듯이 투자자가 주사위게임에서 항상 투자금의 전부를 베팅하면 결국 아무런 수익도 얻지 못하지만, 투자금의 절반만 베팅하고 절반은 현금으로 보유하는 50:50 리밸런싱을 하면 높은 수익을 누적해서 얻을 수 있다. 이러한 과정이 마치 도깨비와 같다고 해서 ‘섀넌의 도깨비’라는 이름이 붙여졌다. 이는 주식투자에서도 똑같이 적용된다.

산술평균은 기하평균보다 크거나 같다. 섀넌은 이 점에 착안했다. 위의 그림처럼 a와 b라는 자산에 투자하는 경우에 산술평균은 파란색 삼각형으로 기하평균은 주황색 삼각형으로 도식화해보자.

앞서 산술평균 수익률과 기하평균 수익률을 비교하면서 연속된 투자를 할 때는 기하평균 수익률을 이용해야 한다고 말했다. 만약 기하평균을 조절할 수 있다면 어떨까? 그림의 반원에서 주황색 점선을 움직여서 파란색 점선으로 맞춘다면 기하평균도 산술평균에 가까워져 점점 더 커지게 된다. 투자할 때 기하평균 수익률을 커지게 만드는 방법도 이와 같다. 동전던지기 게임에서 섀넌은 투자금의 절반만 베팅해서 현금 비중을 늘려서 산술평균 기댓값을 감소시키고 기하평균 기댓값은 증가시켰다.

정리하면 주사위던지기 게임에서 주사위를 던질 때마다 투자금을 모두 투자하는 경우는 산술평균 기댓값이 1.75이고 기하평균 기댓값은 1이다. 주사위던지기는 랜덤워크를 따라서 변동성이 크지만, 투자금은 늘어나지 않는다. 섀넌은 주사위를 던질 때마다 절반의 현금을 보유하고 절반의 투자금만 베팅함으로써 산술평균 기댓값은 1.125로 낮아졌지만, 기하평균 기댓값을 1.06으로 높였고 게임을 할 때마다 6%의 복리수익률을 기대할 수 있는 게임으로 변경시켰다.

이렇게 투자할 때 기하평균 기대수익률이 1이상이 되도록 투자하는 자산들의 비중을 조절해야 장기적으로 자산을 우상향시킬 수 있다. 복리로 자산을 불리기 위해 기하평균 수익률을 이해하고 기하평균 수익률을 높이기 위한 분산투자와 비중조절을 이해하고 실전 투자에 실천하는 것은 성공적인 투자를 위한 기본이다. 이번까지 연이어서 투자의 기본지식을 살펴봤다. 투자의 기초지식에 대한 다른 이야기들도 앞으로 기회가 되는대로 다뤄보도록 하겠다.